Asal Çarpanlar

Asal çarpanlar konusuna geçmeden önce çarpanlar konusu için bir tanım yapalım. Çarpanlar, başka bir sayıyı elde etmek için birbiri ile çarpılan sayılardır. Bu bir sayının tüm çarpanlara bölünmesinin 0 kalanla sonuçlanacağı anlamına gelir. Aynı zamanda bir sayının çarpanı demek, o sayının tam böleni demektir. Peki asal çarpanlar nedir? Bir sayının asal olan çarpanlarına o sayının asal çarpanları denir. Bunu daha iyi anlamak için iki farklı örnek yapalım.

Örnek 1:

24’ün çarpanlarını bulalım.

Çözüm:

24’ün çarpanları 1, 2, 3, 4, 6, 8, 12 ve 24’tür. Bu çarpanlar arasında 2 ve 3 asal sayıdır. Bu durumda 24’ün asal çarpanları 2 ve 3’tür.

Örnek 2:

26’nın çarpanlarını bulalım.

Çözüm:

26’nın çarpanları 1, 2, 13 ve 26’dır. Bu çarpanlar arasında 2 ve 13 asal sayıdır. Bu durumda 26’nın asal çarpanları 2 ve 13’tür.

Asal Çarpanlar Nasıl Bulunur

Asal çarpanlar nasıl bulunur öğrenmek için kullanabileceğimiz iki farklı yöntem bulunmaktadır. Bu yöntemlerden biri için önce sayının çarpanları bulunur ve bu çarpanlar arasından asal olan sayılar alınırak asal çarpanlar olarak kabul edilir. Diğer yöntemde ise sayıyı en küçük asal sayıdan başlayarak sayının kendisine kadar çarpanlarını kullanarak böleriz ve sayıdan geriye 1 kalıncaya kadar bu işleme devam ederiz. Sonuç olarak bulduğumuz asal sayılar da sayının asal çarpanları kabul edilir. Bu yöntemleri aşağıdaki iki farklı örneğe bakarak daha iyi anlayabilirsiniz.

Hatırlatma – Eğer bir sayının sadece iki çarpanı varsa veya sadece 1 ile kendisine bölünebiliyorsa bu asal sayı olduğu anlamına gelir.

Örnek 1:

6 sayısının asal çarpanlarını bulalım.

Yöntem 1:

6 sayısının çarpanları veya 6 sayısının kalansız tam bölenleri 1, 2, 3 ve 6’dır. Bu sayılardan 2 ile 3 sayısı asal sayı olduğu için bu sayılara 6 sayısının asal çarpanları deriz.

Yöntem 2:

6 sayısını en küçük asal sayıdan başlayarak sonuçta 1 oluncaya kadar böleceğiz. Elbette kalansız bölen asal sayıları kullanarak bunu yapacağız ve bunu 6 sayısından geriye 1 kalıncaya kadar devam ettireceğiz. Öncelikle en küçük asal sayı ile başlıyoruz. Bu 2’dir ve 6 sayısı 2 ile tam bölünür. 6’yı 2’ye böldüğümüzde sonuç 3’tür. 6’yı 2’ye böldüğümüz için elimizde artık 6 yerine 3 sayısı var. Şimdi 3 sayısını en küçük asal sayıya bölmeyi deneyeceğiz. 3 sayısını 2’ye bölmeyi deniyoruz ancak 3, 2’ye tam olarak bölünmez. Bu durumda sonraki asal sayıyı yani 3’ü deniyoruz. 3 sayısı 3’e tam bölünür ve 3’ü 3’e böldüğümüzde ise sonuç 1 olur. Amacımız 1 kalıncaya kadar devam etmekti. Bunu yaptık ve yöntemimize uygun olarak asal sayıları da bulmuş olduk. Bu durumda 6 sayısının asal çarpanları 2 ve 3’tür.

Asal Çarpanlar Listesi

100’e kadar olan sayıların asal çarpanları aşağıdaki tabloda verilmiştir.

Sayı	Asal Çarpanlar	Sayı	Asal Çarpanlar	Sayı	Asal Çarpanlar
2	2	35	5, 7	68	2².17 –> 2, 17
3	3	36	2².3² –> 2, 3	69	3, 23
4	2² –> 2	37	37	70	2, 5, 7
5	5	38	2, 19	71	71
6	2, 3	39	3,13	72	2³.3² –> 2, 3
7	7	40	2³.5 –> 2, 5	73	73
8	2³ –> 2	41	41	74	2, 37
9	3² –> 3	42	2, 3, 7	75	3.5² –> 3, 5
10	2, 5	43	43	76	2².19 –> 2, 19
11	11	44	2².11 –> 2, 11	77	7, 11
12	2².3 –> 2, 3	45	3².5 –> 3, 5	78	2, 3, 13
13	13	46	2, 23	79	79
14	2, 7	47	47	80	2⁴.5 –> 2, 5
15	3, 5	48	2⁴.3 –> 2, 3	81	3⁴
16	2⁴ –> 2	49	7², > 7	82	2, 41
17	17	50	2.5² –> 2, 5	83	83
18	2.3² –> 2, 3	51	3, 17	84	2².3.7 –> 2, 3, 7
19	19	52	2².13 –> 2, 13	85	5, 17
20	2².5 –> 2, 5	53	53	86	2.43
21	3, 7	54	2.3³ –> 2, 3	87	3, 29
22	2, 11	55	5, 11	88	2³.11 –> 2, 11
23	23	56	2³.7 –> 2, 7	89	89
24	2³.3 –> 2, 3	57	3, 19	90	2.3².5 –> 2, 3, 5
25	5² –> 5	58	2, 29	91	7, 13
26	2, 13	59	59	92	2².23 –> 2, 23
27	3³ –> 3	60	2².3.5 –> 2, 3, 5	93	3, 31
28	2².7 –> 2, 7	61	61	94	2, 47
29	29	62	2.31	95	5, 19
30	2, 3, 5	63	3².7 –> 3, 7	96	2⁵.3 –> 2, 3
31	31	64	2⁶ –> 2	97	97
32	2⁵ –> 2	65	5, 13	98	2.7² –> 2, 7
33	3, 11	66	2, 3, 11	99	3².11 –> 3, 11
34	2, 17	67	67	100	2².5² –> 2, 5

Bir Sayının Asal Çarpanları Nasıl Bulunur?

Belirli bir sayının asal çarpanlarını bulmanın iki önemli yöntemi vardır. Bunlar:

Bölme Yöntemiyle Asal Çarpanlar
Çarpan Ağacını Kullanan Asal Çarpanlar

Bu iki yöntemi kullanarak bir sayının asal çarpanlarını nasıl bulacağımızı örneklerle birlikte öğrenelim.

Aşağıdaki şekil, çarpan ağacını kullanarak 1092’nin asal çarpanını göstermektedir.

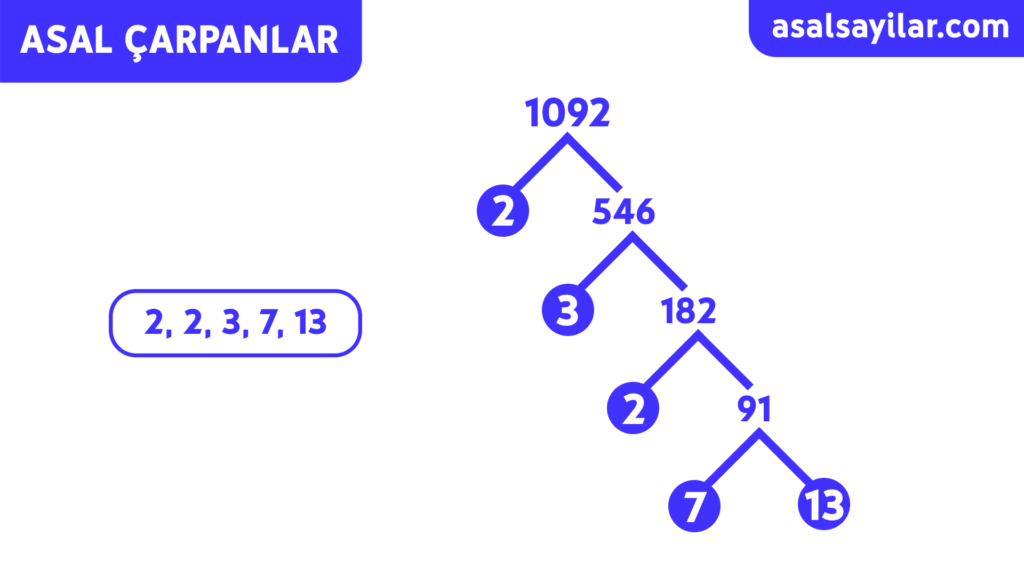
Asal Çarpanlara Ayırma

Herhangi bir sayı asal çarpanlarının çarpımı şeklinde yazılabilir. Bu, asal çarpanlara ayırma olarak bilinir.

Asal çarpanlar, çarpan ağacı açısından da anlaşılabilir. Sayıyı bir ağacın tepesi olarak hayal edin ve onun farklı çarpanlarını temsil eden dallar oluşturarak ilerleyin.

Örneğin, 90’ı alın. 2 * 45 olur. Şimdi 45’i alın, bu 5 * 9 olur. Yine 9, 3 * 3 olur. Dolayısıyla 90, 2 * 3 * 3 * 5’tir. Yani 90, en üstte olur. 2, 3, 3 ve 5 ise 45’in farklı dallarıdır. Ve sayılar daha fazla parçalanamadığı için dallar burada biter.

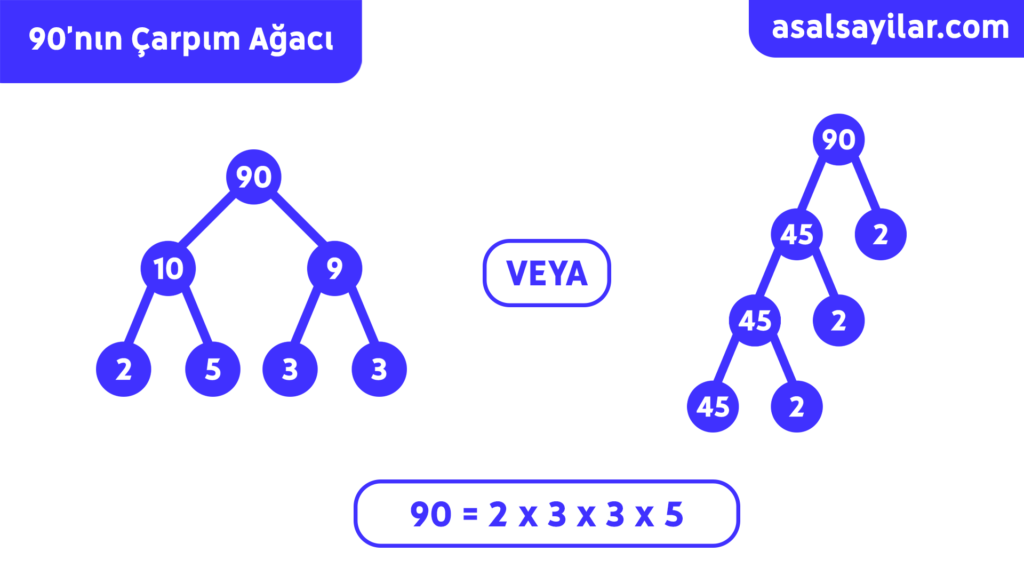
Yukarıdaki örnekte gösterildiği gibi, sayılar çeşitli şekillerde kategorize edilebilir. Tam sayılara, ondalık sayılara ve kesirlere zaten aşinasınız, ancak sayıların dikkate alınması yararlı olabilecek başka özel özellikleri de vardır. Sayılar çift veya tek, tam kareler, tekrar eden veya tekrar etmeyen ondalık sayılar olarak sınıflandırılabilir.

Bir sayının asal çarpanlarını bulmanın çarpan ağacından başka bir yöntemi de kısa bölme yöntemidir.

Bu yöntemi kullanarak 60’ın asal çarpanlarını bulalım.

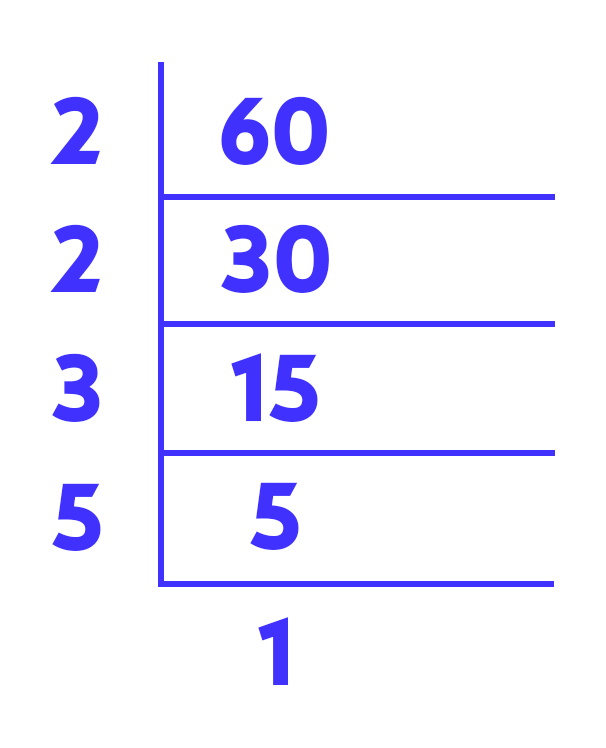
60 = 2 × 2 × 3 × 5

Kısa bölme yöntemi, belirli sayıların En Küçük Ortak Katını bulmak için de kullanışlıdır.

Çözülmüş Örnek

Örnek – 114’ün tüm asal çarpanlarını bulun.

Çözüm – Bir çarpan ağacı oluştururken;

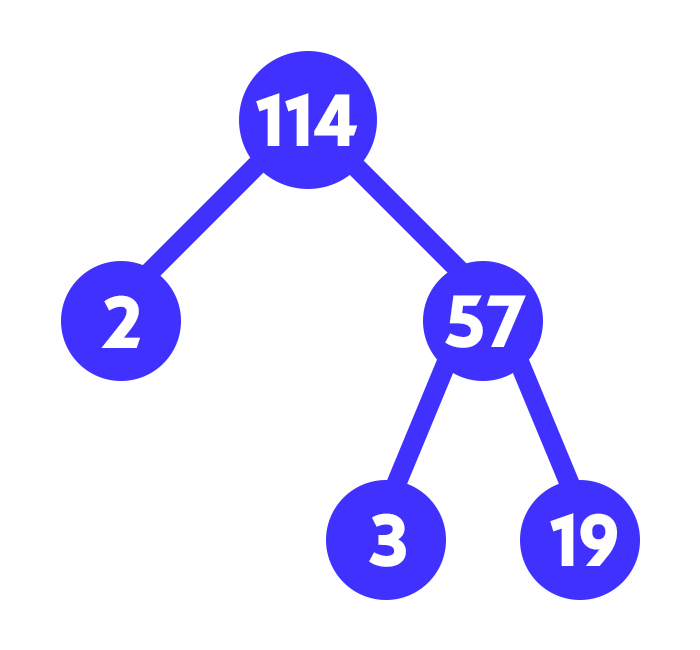
Şeklinde oluşturulur. Buradan, 114’ün asal çarpanları olarak 2, 3 ve 19 asal sayıları bulunur.

Yani 114 = 2 × 3 × 19

Alıştırma Soruları

36’nın asal çarpanlarını yazınız.
24’ün asal çarpanları nelerdir?
72’nin asal çarpanlarını bulun.
Bölme yöntemini kullanarak 5005’in asal çarpanları nasıl hesaplanır?
Çarpan ağacını kullanarak 12 ve 48’in asal çarpanlarını bulun.